课题

《组合图形的面积》

根据反馈调整

教学目标提示

1、使学生能根据组合图形的特点，运用制补的方法正确计算组合图形的面积，并能解释自己的想法。

2、使学生通过解决组合图形面积的计算，，灵活运用不同方法计算同一个组合图形的面积、体会转化思想，感受解决问题方法的多样性，发展思维的深刻性和灵活性。

3、使学生体会数学知识、方法在解决问题中的作用,感受数学知识和方法的价值，培养应用意识:激发学习数学的兴趣。

1. 计算组合图形的面积，可以采用转化的思路，用分割或添补的方法把原来图形转化为规则图形计算面积。大家还有不少的收获

2.还有的交流解决问题可以从不同的角度观察、思考，用不同的方法解决，这
让大家了解了可以灵活地运用知识解决问题;还有的交流要根据实际情况采用合适的算法.

素材与策略

一、复习导入

依次出示长方形、正方形、平行四边形、三角形和梯形，让学生说一说每个图形的面积计算公式。

提问：在用公式计算三角形和梯形的面积时，需要注意什么？使学生通过解决组合图形面积的计算，

，灵活运用不同方

法计算同一

个组合图形的面积、体会转化思想，感受解决问题方法的多样性:

性，发展思维

的深刻性和灵活性。

3.使学生体会数学知识、方法在解决问题

中的作用,感受数学知识和方

法的价值，培养应用意识:激发学习数学的兴趣。使学生通过解决组合图形面积的计算，

，灵活运用不同方

法计算同一

个组合图形的面积、体会转化思想，感受解决问题方法的多样性:

性，发展思维

的深刻性和灵活性。

3.使学生体会数学知识、方法在解决问题

中的作用,感受数学知识和方

法的价值，培养应用意识:激发学习数学的兴趣。使学生通过解决组合图形面积的计算，

，灵活运用不同方

法计算同一

个组合图形的面积、体会转化思想，感受解决问题方法的多样性:

性，发展思维

的深刻性和灵活性。

3.使学生体会数学知识、方法在解决问题

中的作用,感受数学知识和方

法的价值，培养应用意识:激发学习数学的兴趣。出示一个组合图形，请同学观察，思考如何计算面积。

揭题：今天这节课我们来学习组合图形的面积计算。

二、自主探索 发现规律

1.出示例题，初步探索。

例10：华丰小学的校园里有一块草坪，它的面积是多少平方米？

让学生读题，说说题里的条件和问题。

说明:这样的图形能不能用哪个面积计算公式直接计算?

2.探索算法,解决问题。

引导;这样的图形不是以前认识过的图形，形状是不规则的，但它可能是一些认识过的规则图形组合起来的，一般叫它组合图形。(板书:组合图形）题里的组合图形不能直接用公式计算，那大家想想可以怎样计算，把你的想法和同桌交流。

交流:你准备怎样算？说说你的想法。

结合交流，直观呈现图形表示不同思路，引导学生理解不同分割和添补的解题方法。

反馈不同想法，引导学生找到相关数据。

预设：

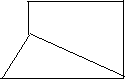
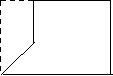
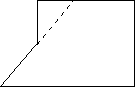
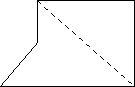
          S组合＝S长方形＋S梯形               S组合＝S三角形＋S长方形

     S组合＝S三角形＋S梯形               S组合＝S长方形－S梯形

在此过程中，指导学生说出：把这个图形分成         和         ，这个图形的面积就是这个        和         的面积之和；把这个图形补成一个         ，这个图形的面积就是         和         的面积之差。  

3.比较总结，列式计算。

提问：比较刚才四种想法，有什么不同的地方和相同的地方？

不同：（1）有的是分割成两个基本图形，有的是补一个基本图形变成另一个基本图形。（2）可以有不同的分割方法。

相同：不管是分割还是添补，都是把组合图形转化成基本图形。

分或补

板书：组合图形              基本图形

                  转化

出示不常用的分割方法，让学生说说想法。

提醒：计算组合图形面积，要转化成基本图形，并且能找到基本图形相应的数据，还应该选择便于计算的方法。

让学生选择一种想法求出这个组合图形的面积。

学生独立计算，教师巡视，指名学生板演，交流检验。

4.回顾反思。

提问：如何计算一个组合图形的面积？分或者补要注意什么？

指出：计算组合图形的面积一般要把组合图形利用分或者补转化成已经学过的基本图形，再把各部分相加或者相减；分或者补时，第一要注意分或者补成的基本图形要是规则图形，可以直接利用公式计算各部分面积，第二要注意分或者补的图形，计算基本图形的面积时能找到相应的数据，第三要注意分或者补的方法有多种，应该选择便于计算的方法。（板书：规则图形 具备条件 不同方法）

三、练习巩固

出示练一练：

让学生读题、观察，独立思考、完成计算。

交流:你是怎样计算的? (结合交流呈现割补方法并板书算式，结合图形说明每一步计算的是什么)

追问:为什么最后一步有的计算用加法 ,有的计算用减法?

说明:计算组合图形的面积，可以通过转化变成规则图形计算，转化的万法可以不同，只要是能计算出面积的方法都可以。但要注意，如果用分割的方法转化，要把分制成的几个部分相加:板书:分期用加法)如果用涂补的方法转化，要用添补成的规则图形面积减去添补部分的面积。(板书:深补用减法)

2.做练习四第2题。
学生独立解答,指名板演。
交流:计算这块草坪的面积是怎样想的? (说明思路、检查计算结果)。

四、课堂小结

提问：今天这节课，你有了什么新的收获？

指出：解决问题时，我们可以把新问题转化成我们之前熟悉的问题来解决。在计算组合图形的面积时，可以利用用分或者补的方法把组合图形转化成基本图形，再分别求出基本图形的面积，把基本图形的面积相加或者相减。如果是把组合图形分割，则要把基本图形面积相加，如果是用一个基本图形把组合图形补拼成另一个基本图形，则要把基本图形面积相减。

五、布置作业

完成《补充习题》P13

六、板书设计 ：

组合图形的面积

          S组合＝S长方形＋S梯形               S组合＝S三角形＋S长方形

     S组合＝S三角形＋S梯形               S组合＝S长方形－S梯形

分或补

板书：组合图形              基本图形

                  转化

规则图形 具备条件 不同方法

教 后 小 记

本节课，通过体验、探究使学生通过解决组合图形面积的计算，灵活运用不同方

法计算同一个组合图形的面积、体会转化思想，感受解决问题方法的多样性，发展思维

的深刻性和灵活性。

使学生体会数学知识、方法在解决问题中的作用,感受数学知识和方法的价值，培养应用意识:激发学习数学的兴趣。